โจทย์พาราโบลา ม.3

โจทย์พาราโบลา ระดับชั้นมัธยมต้น โดยจะเป็นตัวอย่างโจทย์เพื่อฝึกฝนและเสริมความเข้าใจ ไม่ได้กล่าวถึงเนื้อหา เพราะฉะนั้นใครที่ยังไม่เคยเรียนเรื่อง พาราโบลา แนะนำให้กลับไปทบทวนก่อนที่จะมาอ่านในหัวข้อตัวอย่างนี้
ขั้นตอนการเรียน
- อ่านโจทย์ให้เข้าใจ
- ลองทำในกระดาษหรือสมุดก่อนดูเฉลย
- ตรวจสอบกับเฉลย
- สรุปความเข้าใจ
เนื้อหาทั้งหมดของ พาราโบลา
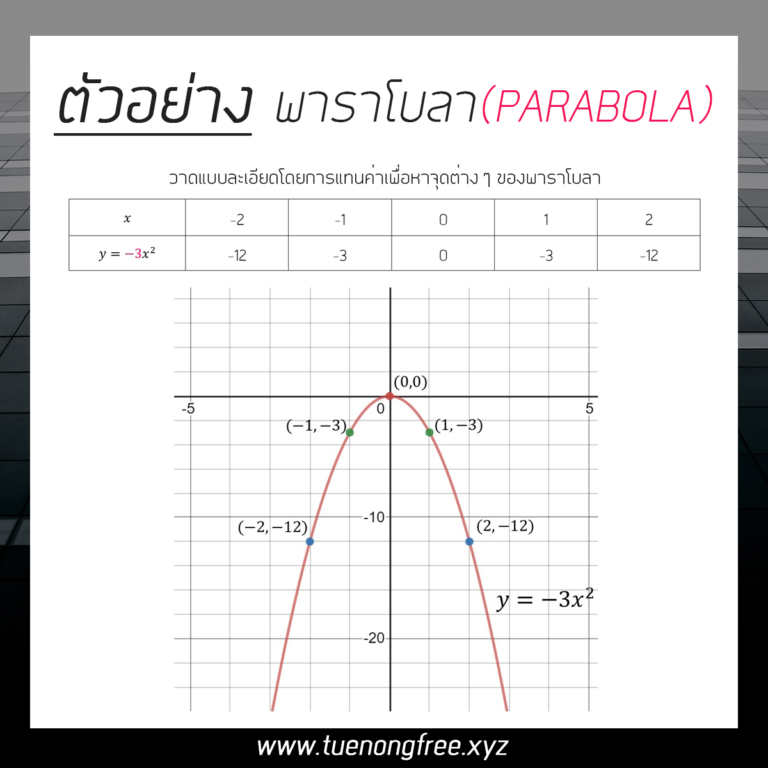
ตัวอย่างที่ 1 จงเขียนกราฟของสมการต่อไปนี้ y = -3x2
พิจารณา สมการ y = -3x2 y=ax2
เพราะฉะนั้น a = -3
จะได้ว่า
a < 0 เป็นพาราโบลา คว่ำ
จุดสูงสุด อยู่ที่จุด (0,0)
แกนสมมาตรอยู่ที่ x = 0

ตัวอย่างเพิ่มเติม แบบฝึกหัด สมการพาราโบลา รูปแบบที่ 1
ตัวอย่างที่ 2 จงเขียนกราฟของสมการต่อไปนี้ y = 5x2+4
พิจารณา สมการ y = 5x2+4 y=ax2+k
เพราะฉะนั้น a = 5 , k = 4
จะได้ว่า
a > 0 เป็นพาราโบลา หงาย
จุดต่ำสุด อยู่ที่จุด (0,4)
แกนสมมาตรอยู่ที่ x = 0


ตัวอย่างเพิ่มเติม แบบฝึกหัด สมการพาราโบลา รูปแบบที่ 2
ตัวอย่างที่ 3 จงเขียนกราฟของสมการต่อไปนี้ y = -5(x+2)2
พิจารณา สมการ y = -5(x+2)2 y = a(x-h)2
เพราะฉะนั้น a = -4 , h = -2
จะได้ว่า
a < 0 เป็นพาราโบลา คว่ำ
จุดสูงสุด อยู่ที่จุด (-2,0)
แกนสมมาตรอยู่ที่ x = -2


ตัวอย่างเพิ่มเติม แบบฝึกหัด สมการพาราโบลา รูปแบบที่ 3
ตัวอย่างที่ 4 จงเขียนกราฟของสมการต่อไปนี้ y = (1/3)(x-1)2-2
พิจารณา สมการ y = (1/3)(x-1)2-2 y = a(x-h)2+k
เพราะฉะนั้น a = (1/3) , h = 1 , k = -2
จะได้ว่า
a > 0เป็นพาราโบลา หงาย
จุดต่ำสุด อยู่ที่จุด (1,-2)
แกนสมมาตรอยู่ที่ x = 1


ตัวอย่างเพิ่มเติม แบบฝึกหัด สมการพาราโบลา รูปแบบที่ 4
ตัวอย่างที่ 5 จงเขียนกราฟของสมการต่อไปนี้ y=x2+6x+8
จากสมการ y=x2+6x+8
เขียนสมการให้อยู่ใน รูปสมการพาราโบลา ได้ดังนี้
y=x2+6x+8
= (x2+6x+32-32)+8
= (x2+6x+32)-32+8
= (x+3)2-9+8
= (x+3)2-1
จะได้ว่า แปลงจากสมการ y=x2+6x+8 y = (x+3)2-1
พิจารณา สมการ y = (x+3)2-1 y = a(x-h)2+k
เพราะฉะนั้น a = 1 , h = -3 , k = -1
จะได้ว่า
a > 0 เป็นพาราโบลา หงาย
จุดต่ำสุด อยู่ที่จุด (-3,-1)
แกนสมมาตรอยู่ที่ x = -3