เอกนาม

เนื้อหา เอกนาม
ในเรื่องของ เอกนาม จะมีสิ่งสองสิ่งที่แตกต่างกัน เราจำเป็นต้องแยกให้ออกก่อนที่จะทำโจทย์เพื่อให้เกิดความถูกต้องและรวดเร็วในการทำโจทย์ นั่นคือ ตัวแปรและค่าคงตัว
- ตัวแปร หมายถึง สิ่งที่ไม่สามารถระบุจำนวนทางคณิตศาสตร์ได้ หรือกล่าวง่าย ๆ คือ สัญลักษณ์ที่แทนตัวเลขใด ๆ มักจะใช้เป็นตัวอักษรภาษาอังกฤษ เช่น x , y , A , B , C หรืออื่น ๆ
- ค่าคงตัว หมายถึง ตัวเลขที่ทราบค่าได้อย่างแน่ชัด กล่าวง่าย ๆ คือ ตัวเลข , หรือสัญลักษณ์ที่เราทราบค่าแน่นอน เช่น 2 , 5 , -3 , π เป็นต้น (π มีค่าประมาณ 3.14)
เนื้อหาทั้งหมดของ พหุนาม
ดูเนื้อหาเอกนามบน Youtube
อย่างที่ได้กล่าวมา ส่วนที่สำคัญที่สุดในการทำโจทย์เรื่อง พหุนาม คือ ต้องสามารถแยกระหว่าง ตัวแปร กับ ค่าคงที่ ให้ได้ก่อน เพราะฉะนั้นมาลองดูตัวอย่างกัน
ตัวอย่าง | |
5x | |
ค่าคงตัว | ตัวแปร |
5 | X |
ตัวอย่าง | |
-9A2B | |
ค่าคงตัว | ตัวแปร |
-9 | A2B |
ตัวอย่าง | |
r2h | |
ค่าคงตัว | ตัวแปร |
– | r2h |
ข้อควรรู้
- เมื่อมีค่าคงตัวเป็น 1 มักไม่เขียน และถ้าค่าคงตัวเป็น -1 มักเขียนแค่เครื่องหมาย – อยู่หน้าสุด
- เมื่อมีค่าคงที่หลายตัว มักคูณค่าคงตัวก่อน แล้วเขียนผลลัพธ์ไว้หน้าสุด

เอกนาม ( Monomail )
เอกนาม คือ นิพจน์ที่เขียนอยู่ในรูปการคูณของค่าคงตัวกับตัวแปรอย่างน้อยหนึ่งตัว และมีเลขชี้กำลังเป็นจำนวนเต็มบวก หรือ ศูนย์
สัมประสิทธิ์ของเอกนาม
คือ ค่าคงตัวในเอกนาม
ดีกรีของเอกนาม
คือ ผลรวมของเลขชี้กำลังของตัวแปรทุกตัวในเอกนาม
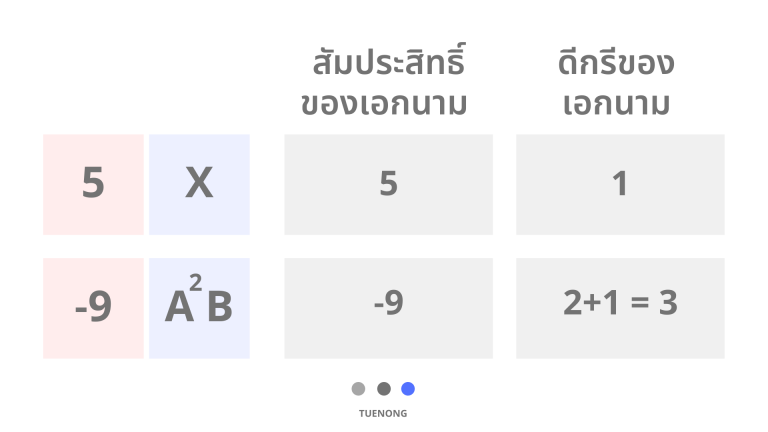
ตัวอย่าง | |
5x | |
สัมประสิทธิ์ของเอกนาม | ดีกรีของเอกนาม |
5 | 1 |
ตัวอย่าง | |
-9A2B | |
สัมประสิทธิ์ของเอกนาม | ดีกรีของเอกนาม |
-9 | 2+1=3 |
ตัวอย่าง | |
3a2bc3 | |
สัมประสิทธิ์ของเอกนาม | ดีกรีของเอกนาม |
3 | 2+1+3=6 |
การบวกและลบของเอกนาม
เอกนาม สามารถบวกและลบกันได้ โดยมีกฎเหล็ก เพียงข้อเดียวที่ต้องตรวจสอบก่อนทำการบวกลบ คือ
” เอกนามจะสามารถบวกและลบกันได้ เมื่อตัวแปรเหมือนกัน “
กล่าวคือ จะบวกหรือลบเอกนาม เอกนามทั้งสองต้องมีตัวแปรที่เหมือนกัน รวมถึงเลขชี้กำลังต้องเท่ากัน
การบวกเอกนาม
ถ้าเอกนามมีตัวแปรเหมือนกัน ให้นำสัมประสิทธิ์ของเอกนามมาบวกกัน
การลบเอกนาม
ถ้าเอกนามมีตัวแปรเหมือนกัน ให้นำสัมประสิทธิ์ของเอกนามมาลบกัน
หมายเหตุ ถ้ายังแยกไม่ออกว่า สัมประสิทธิ์ของเอกนามคืออะไร ให้กลับไปทบทวนเรื่อง เอกนามก่อน


ตัวอย่าง จะหาผลบวกของ 4x2y + 7x2y
เอกนามจะสามารถบวกกันได้ เมื่อตัวแปรเหมือนกัน
= (4+7)x2y = 11x2y
ตัวอย่าง จะหาผลลบของ 4x2y – 7x2y
เอกนามจะสามารถลบกันได้ เมื่อตัวแปรเหมือนกัน
= (4-7)x2y = -3x2y
ตัวอย่าง จะหาผลบวกของ 5xy3 + 7x2y
เอกนามจะสามารถบวกกันได้ เมื่อตัวแปรเหมือนกัน
ข้อนี้มีตัวแปรต่างกัน จึงไม่สามารถบวกกันได้

