พื้นฐานการแตกแรง

พื้นฐานเรื่อง เวกเตอร์และการแตกแรง

สำหรับเนื้อหาเรื่อง เวกเตอร์ จะอธิบายถึงความหมายของปริมาณทางฟิสิกส์ที่บอกถึงปริมาณเวกเตอร์และสเกลาร์รวมถึงพื้นฐานของปริมาณเวกเตอร์ต่างๆเช่น การหาแรงลัพธ์ แตกแรง ในรูปแบบต่างๆ การรวมแรงเป็นบทพื้นฐานที่สำคัญในวิชาฟิสิกส์ที่จะต้องนำไปใช้ในวิชาฟิสิกส์ ต่อไปอีกหลายๆบทเพราะฉะนั้นเรามาทำความเข้าใจเรื่องเวกเตอร์และ แตกแรง กันดีกว่า

ปริมาณทางฟิสิกส์

ปริมาณในทางฟิสิกส์แบ่งเป็นด้วยกันทั้งหมด 2 ปริมาณ คือ

ปริมาณเวกเตอร์ คือ ปริมาณที่บอกทั้งขนาด และ ทิศทาง
ปริมาณสเกลาร์ คือ ปริมาณที่บอกเพียงแค่ขนาดเพียงอย่างเดียว

การหาขนาดและทิศทางของแรงลัพธ์

การหาขนาดและทิศทางของเวกเตอร์ลัพธ์ สามารถแบ่งออกได้เป็น 4 รูปแบบใหญ่ๆเลยคือ

เวกเตอร์ทิศทางเดียวกัน
เวกเตอร์ทิศทางตรงกันข้ามกัน
เวกเตอร์ตั้งฉากกัน
เวกเตอร์ทำมุมกัน

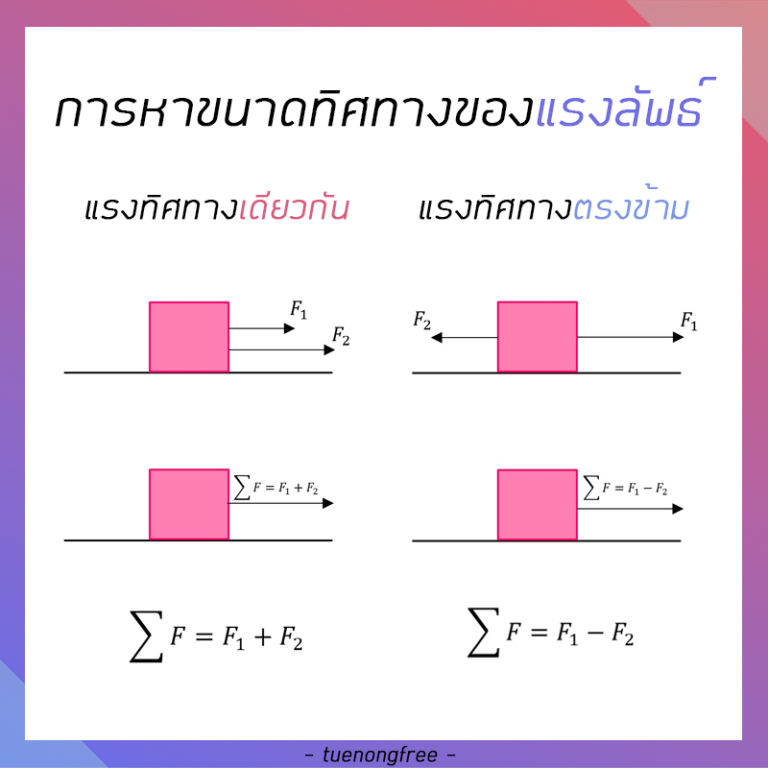
เวกเตอร์ทิศทางเดียวกัน

การหาเวกเตอร์ลัพธ์ของแรงทิศทางเดียวกันสามารถหาได้ โดยการนำเวกเตอร์ที่มีทิศทางเดียวกันนั้น นำขนาดมาบวกกัน รวมกันเป็นเวกเตอร์ลัพธ์ที่มีทิศทางเหมือนกับทิศทางเดิม

เวกเตอรืทิศทางตรงข้าม

การหาเวกเตอร์ลัพธ์ของแรงทิศทางตรงข้ามกันสามารถหาได้ โดยการนำเวกเตอร์ที่มีทิศทางตรงข้ามกันนั้น นำขนาดมาลบกัน รวมกันเป็นเวกเตอร์ลัพธ์ที่มีทิศทางเหมือนกับทิศทางเดิมที่มีขนาดมากกว่า

การรวมเวกเตอร์ 2 มิติ

ในกรณีที่เวกเตอร์ไม่ได้ไปในทิศทางเดียวกัน หรือ ทิศทางตรงกันข้าม เราสามารถหาเวกเตอร์ลัพธ์โดยการคำนวณได้โดยสามารถแบ่งเป็น 2 กรณีคือ เวกเตอร์ที่ตั้งฉากกัน กับเวกเตอร์ที่ทำมุมกัน

การรวมเวกเตอร์ 2 มิติ ที่ตั้งฉากกัน

สูตรหาขนาด

R = √P²+Q²

สูตรหามุม

tan θ = Q/P

โดยที่

R คือ เวกเตอร์ลัพธ์

P คือ เวกเตอร์ย่อย

Q คือ เวกเตอร์ย่อย

θ คือ มุมที่เวกเตอร์ลัพธ์กระทำกับแนวราบ

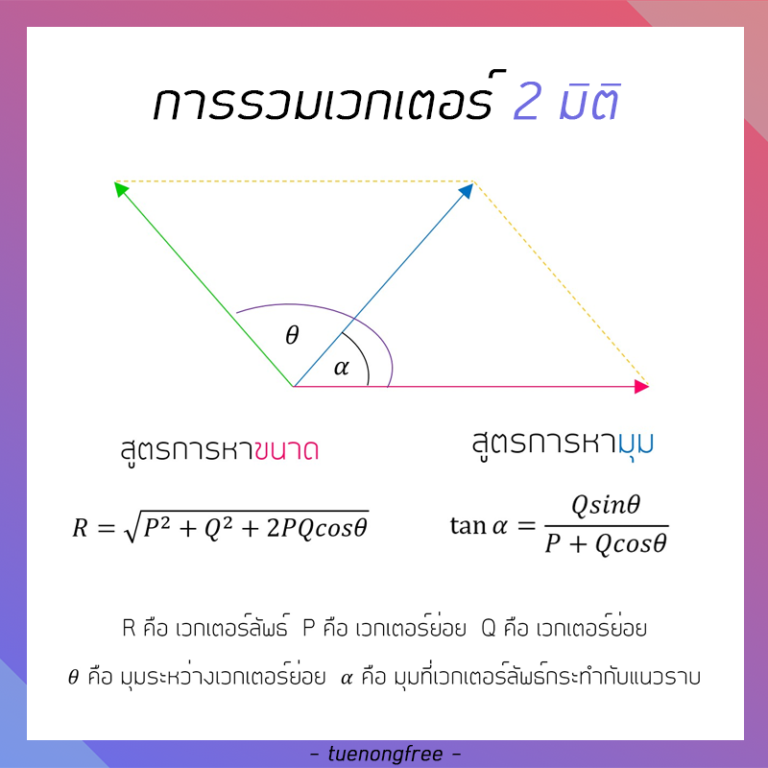
การรวมเวกเตอร์ 2 มิติ ที่ตั้งทำมุมกัน

สูตรหาขนาด

R = √P²+Q²+2PQ cosθ

สูตรหามุม

tan θ = Qsinθ/P+Qcosθ

โดยที่

R คือ เวกเตอร์ลัพธ์

P คือ เวกเตอร์ย่อย

Q คือ เวกเตอร์ย่อย

θ คือ มุมที่เวกเตอร์ย่อย

α คือ มุมที่เวกเตอร์ลัพธ์กระทำกับแนวราบ

แตกแรง

แตกแรงคือการนำเวกเตอร์มาแยกเป็นเวกเตอร์ 2 เวกเตอร์ เพื่อให้สามารถ คำนวณได้ง่ายขึ้นในกรณีที่แรงเราทำมุมแตกต่างกับเวกเตอร์อื่น โดยมีจะมีวิธีการทั้งหมด 2 แบบ คือ