สมดุลกล

สภาพสมดุล
เนื้อหาในบทนี้จะพูดหลักๆด้วยเรื่องของ สมดุล ซึ่งเป็นบทประยุกต์จากเรื่องกฎการของที่ของนิวตัน ซึ่งเป็นหัวข้อที่สำคัญมากเพราะมีการนำไปใช้ประโยชน์ได้ในหลายๆศาสตร์เลย ในการเรียนในระดับที่สูงขึ้นในหัวข้อเรื่อง สมดุลกล จะถูกเรียนอย่างจริงจังขึ้นและนำไปประยุกต์ใช้ได้จริงๆ ในหัวข้อนี้ถ้าน้องๆยังไม่ได้เรียนเรื่องกฎการเคลื่อนที่ของนิวตันขอแนะนำให้กลับไปทบทวนก่อนจะช่วยให้เข้าใจบทนี้ได้ง่ายขึ้น
สภาพสมดุล (Equilibrium)
คือ สภาพที่วัตถุสามารถรักษาสภาพการเคลื่อนที่ให้คงเดิม สมดุลกล ที่เกิดขึ้นในขณะที่วัตถุอยู่ในสภาพนิ่ง หรือเคลื่อนที่ด้วยความเร็วคงตัว เช่นอยู่นิ่ง คือทั้งไม่มีการเลื่อนตำแหน่งและไม่หมุน หรือเคลื่อนที่ในสภาพเดิม คือ จุดศูนย์กลางมวลเลื่อนด้วยอัตราเร็วคงที่และหมุนรอบแกนผ่านจุดศูนย์กลางมวลด้วยอัตราเร็วเชิงมุมคงที่ ถ้าแรงลัพธ์ที่กระทำต่อวัตถุมีค่าเป็นศูนย์สภาพสมดุลของวัตถุ คือ การคงสภาพของวัตถุ แบ่งได้ 2 กรณี คือ
สมดุลสถิต (static equilibrium)
คือ สภาพสมดุลของวัตถุอยู่นิ่ง
สมดุลจลน์ (kinetic equilibrium)
คือ สภาพสมดุลของวัตถุที่เคลื่อนที่ด้วยความเร็วคงตัว (a=0)
ลักษณะของสมดุล แบ่งออกเป็น 3 ลักษณะ คือ
- สมดุลต่อการเคลื่อนที่ (translation equilibrium) คือการสมดุลที่วัตถุอยู่นิ่ง ๆ หรือเคลื่อนที่ด้วยความเร็วคงตัว
ΣF = 0
- สมดุลต่อการหมุน (absolute equilibrium) คือ วัตถุมีอัตราการหมุนคงตัวผลรวมของโมเมนต์
ΣM = 0
- สมดุลสัมบูรณ์ (absolute equilibrium) คือ การสมดุลที่มีทั้งสมดุลต่อการเลื่อนตำแหน่งและสมดุลต่อการหมุนและเงื่อนไขของสมดุล
ΣF = 0 และ ΣM = 0
โดยที่
F คือ แรง หน่วยเป็น N
M คือ โมเมนต์ หน่วยเป็น N•m
สมดุลต่อการเคลื่อนที่
อย่างที่ทราบกันว่าสมดุลต่อการเคลื่อนที่คือการสมดุลที่วัตถุอยู่นิ่ง ๆ หรือเคลื่อนที่ด้วยความเร็วคงตัว เพราะฉะนั้นหลักการคือต้องใช้กฎการเคลื่อนของนิวตันให้เป็นไปตามสมการ
ΣF = 0
- กรณีที่มีแรง 2 แรงกระทำต่อวัตถุ จะมีสมดุลเมื่อ
- แรง 2 แรงมีขนาดเท่ากัน แต่มีทิศทางตรงข้ามกัน
- โมเมนต์รอบจุดใดๆ จะเป็น0 ได้ก็ต่อเมื่อแรงทั้งสองอยู่ในแนวเดียวกัน
- กรณีที่มีแรง 3 แรงกระทำ แบ่งได้เป็น 2 กรณี คือ
- แนวแรงทั้ง 3 ขนานกัน และรวมกันแล้วทั้งหมดเป็น 0
- แนวแรงทั้ง 3 ไม่ขนานกัน สภาพสมดุลจะเกิดขึ้นเมื่อ
- 2.1 แรงทั้ง 3 อยู่บนระนาบเดียวกัน
- 2.2 แนวแรงทั้ง 3 ต้องพบกันที่จุด ๆ หนึ่ง
- 2.3 แรงลัพธ์ของแรงทั้ง 3 เป็น 0
- 2.4 โมเมนต์ลัพธ์ของแรงทั้ง 3 เป็น 0
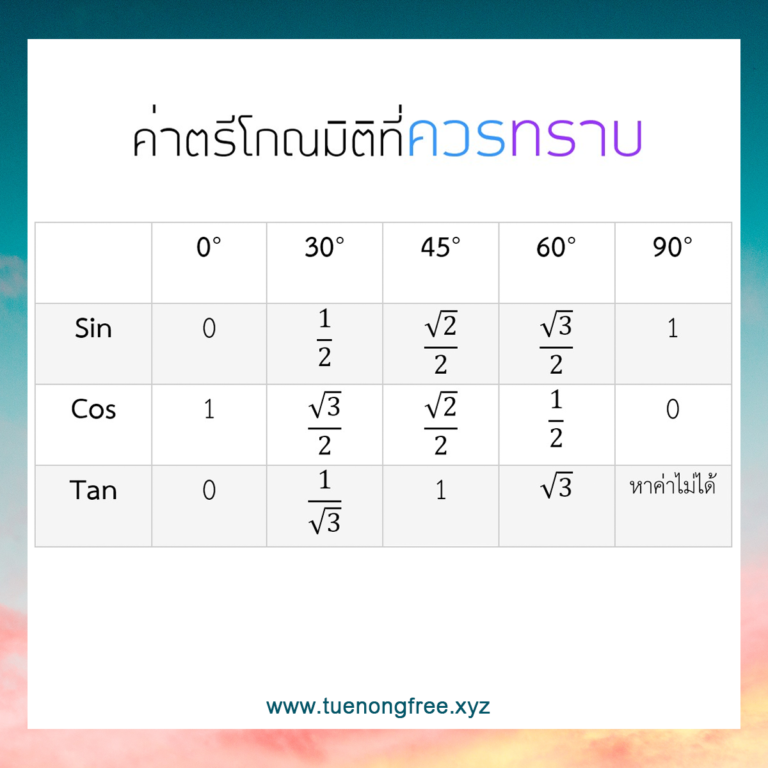
หมายเหตุ : ค่าตรีโกณมิติที่ควรรู้เป็นพื้นฐานในการทำโจทย์ สมดุลกล
ขั้นตอนการแก้โจทย์สมดุลต่อการเคลื่อนที่
1.วาดรูปและเขียนแรงทั้งหมดออกมา
2.แตกแรงทุกแรงเข้าหาแกนอ้างอิง ( แกน x และ แกน y หรือแกนตามลักษณะวัตถุ)
3.รวมแรงตามแนวแกนอ้างอิง ( แกน x และ แกน y หรือแกนตามลักษณะวัตถุ) ต้อง = 0
ΣF = 0
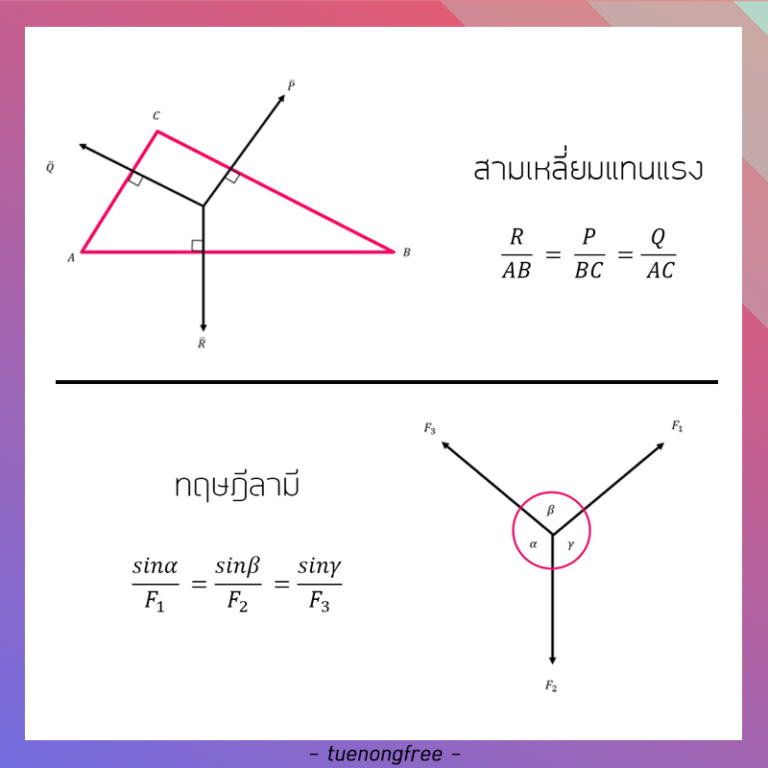
สามเหลี่ยมตั้งฉากแทนแรง
R/AB = P/BC = Q/AC
ทฤษฎีลามี
แรง 3 แรง และมุม 3 มุม ที่ทำให้วัตถุมีสมดุลทฤษฎีบทนี้กล่าวไว้ว่า “ถ้ามีแรง 3 แรงกระทำกับวัตถุ แล้วทำให้วัตถุเกิดสมดุลและแรงทั้งสามพบกันที่จุดๆ หนึ่งแล้ว อัตราส่วนของแรงต่อ sin ของมุมที่อยู่ตรงข้ามของแรงและมุมทั้ง 3 คู่จะเท่ากัน
sinα / F1 = sinβ / F2 = sinγ / F3
ถ้าให้โมเมนต์ตามเข็มนาฬิกามีเครื่องหมายเป็นบวก และโมเมนต์ทวนเข็มนาฬิกามีเครื่องหมายเป็นลบ
สรุปได้ว่า วัตถุที่สมดุลต่อการหมุน ผลรวมทางคณิตศาสตร์ของโมเมนต์จะมีค่าเป็น 0
วัตถุพอดีล้ม
วัตถุพอดีล้มถือได้ว่าเป็นสมดุลของแรงอย่างหนึ่ง
วัตถุล้มบนพื้นราบ
แนวแรงปฏิกิริยา N อยู่ที่ขอบฐานพอดี
ΣMa=0
โมเมนต์ทวนเข็ม = โมเมนต์ตามเข็ม
M ทวน = M ตาม
mg × d =F × h
โดยที่
ΣMa คือ ผลรวมของโมเมนต์ที่จุด A
F คือ แรงเสียดทาน
Mg น้ำหนักของวัตถุ
N คือ แรงปฎิกิริยาตั้งฉาก
h,d คือ ระยะห่างตำแหน่งต่างๆ
วัตถุล้มบนพื้นเอียง
น้ำหนัก (mg) และแรงปฏิกิริยา (N) ผ่านที่ขอบฐานพอดี จากหลักตรีโกณมิติ จะได้







