เซต

สรุปเนื้อหา เซต ระดับ ม. 4 และสำหรับน้อง ๆ ม.ปลาย ที่ต้องการทบทวน โดยจะมีเนื้อหาตั้งแต่ วิธีการเขียนเซต การนับจำนวนสมาชิกในเซต ชนิดของเซต ความสัมพันธ์ระหว่างเซต สมบัติของเซต พาเวอร์เซต สมบัติของพาเวอร์เซต แผนภาพเวนน์-ออยเลอร์ ยูเนียน อินเตอร์เซคชัน คอมพลีเมนต์ และผลต่าง ซึ่งเป็นพื้นฐานในการเรียนที่สำคัญมากเมื่อน้อง ๆ ทบทวนเสร็จ อย่าลืมทำโจทย์เพื่อเสริมความเข้าใจด้วยละ
เนื้อหาทั้งหมดของ เซต
สัญลักษณ์
{ } แทน เซต
∈ แทน คำว่า” เป็นสมาชิก”
∉ แทนคำว่า “ไม่เป็นสมาชิก”
⊂ แทนคำว่า “สับเซต”
⊄ แทนคำว่า ” ไม่เป็นสับเซต”
วิธีการเขียน เซต
- เขียนแบบแจกแจงสมาชิก
A = { a , b , c }
B = { ก , {ข} , {ค,ง}}
- เขียนแบบบอกเงื่อนไข
จะใช้เครื่องหมาย | แทนค่าว่า “โดยที่”
A = { x | x²-4x+3=0 }
การนับจำนวนสมาชิกในเซต
- จำนวนสมาชิกของเซต A เขียนแทนด้วย n(A)
- ถ้าสมาชิกในเซตซ้ำกันให้เขียนเพียงครั้งเดียว
ชนิดของเซต
- เซตจำกัด คือ เซตที่สามารถบอกได้ว่ามีสมาชิกทั้งหมดกี่ตัว
- เซตอนันต์ คือ เซตที่ไม่สามารถบอกได้ว่ามีสมาชิกทั้งหมดกี่ตัว
- เซตว่าง คือ เซตที่ไม่มีสมาชิกในเซตเลย หรือเขียนแทนด้วย ∅
เอกภพสัมพัทธ์ (U) คือ เซตที่กำหนดขอบเขตสิ่งที่เรากำลังพิจารณา
ความสัมพันธ์ระหว่างเซต
- เซตที่เท่ากัน คือ เซตที่สมาชิกทุกตัวเหมือนกัน ถ้าเซต A เท่ากับเซต B จะเขียนแทนด้วยสัญลักษณ์ A = B
- เซตที่เทียบเท่ากัน คือ เซตที่จำนวนสมาชิกเท่ากัน
สมบัติของสับเซต
- ถ้า A⊂B และ A ≠ B จะเรียก A ว่าเป็นสับเซตแท้ของ B
- ถ้า A เป็นเซตจำกัด จะมีสมาชิก n ตัว แล้ว A มีสับเซตทั้งหมด 2n สับเซต
- ถ้า A เป็นเซตจำกัด จะมีสมาชิก n ตัว แล้ว A มีสับเซตแท้ทั้งหมด 2n -1 สับเซต
- Φ ⊂ A (เซตว่างเป็นสับเซตทุกเซต)
- A ⊂ A (ตัวเองก็เป็นสับเซตของตัวเอง)
- ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C
- A ⊂ B และ B ⊂ A ก็ต่อเมื่อ A = B
หมายเหตุ : Φ ( เซตว่าง ) ไม่มีสับเซต
เพาเวอร์เซต
เพาเวอร์เซตของ A คือ เซตที่รวม สมาชิกที่เป็นสับเซตของ A ทั้งหมดเอาไว้
ใช้สัญลักษณ์ P(A)
สมบัติของเพาเวอร์เซต
- P(A) ≠ ∅
- ∅ ∈ P(A)
- ∅ ⊂ P(A)
- A ∈ P(A)
- ถ้า A มีสมาชิก n ตัวแล้ว P(A) มีจำนวนสมาชิกทั้งหมด 2n ตัว
- A ⊂ B ก็ต่อเมื่อ P(A) ⊂ P(B)
- P(A) ∩ P(B) = P(A∩B)
- P(A) ∪ P(B) ⊂ P(A∪B)

การดำเนินการของเซต
คลิปสอน การดำเนินการของเซต
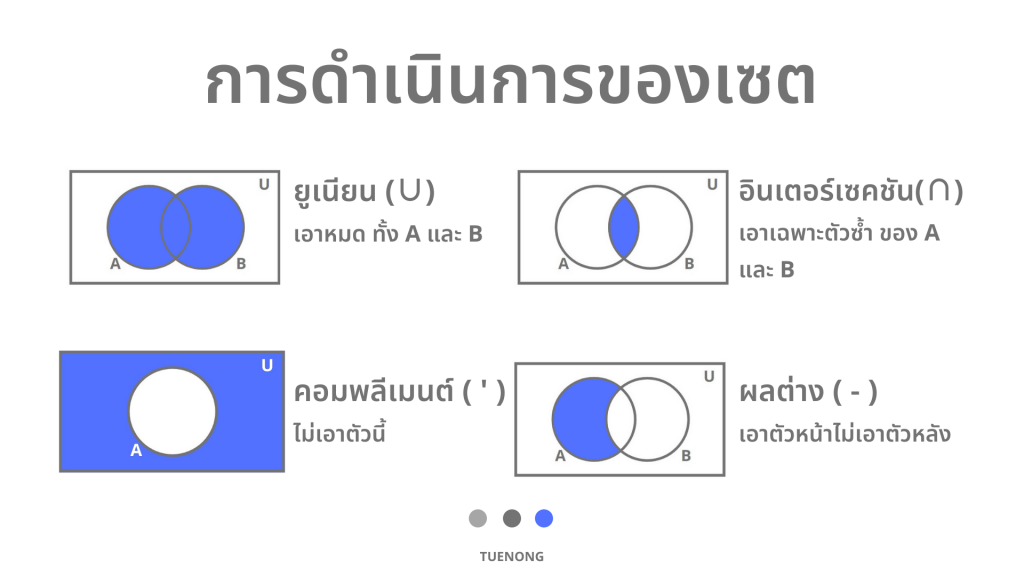
ยูเนียน ( Union ) (เขียนแทนด้วยสัญลักษณ์ ∪)
สมบัติของยูเนี่ยน (กำหนด A , B เป็นเซตใด ๆ )
- A∪B = B∪A
- A∪A = A
- A∪U = U
- A∪∅ = A
- (A∪B)∪C = A∪(B∪C)
- A∪(B∩C) = (A∪B)∩(A∪C)
- A∪A’ = U
- (A∪B)’=A’∩B’
- A-(B∪C) = (A-B)∩(A-C)

อินเตอร์เซคชัน ( Intersection ) (เขียนแทนด้วยสัญลักษณ์ ∩)
คุณสมบัติของอินเตอร์เซค ( กำหนด A,B เป็นเซตใด ๆ )
- A∩B = B∩A
- A∩A = A
- A∩U = A
- A∩∅ = ∅
- (A∩B)∩C = A∩(B∩C)
- A∩(B∪C) = (A∩B)∪(A∩C)
- A∩A’ = ∅
- (A∩B)’ = A’∪B’
- A- (B∩C) = (A-B)∪(A-C)

คอมพลีเมนต์ ( Complement )
คุณสมบัติของคอมพลีเมนต์
- (A’)’ = A ; Aคู่’ = A
- ((A’)’)’ = A’ ; Aคี่’ = A’
- ∅’ = U
- U’ = ∅
- A∪A’ = U
- A∩A’ = ∅
- A⊂B ก็ต่อเมื่อ B’⊂A’
- A∩B = ∅ ก็ต่อเมื่อ A’⊂B’

ผลต่าง ( Differrence )
คุณสมบัติของผลต่างระหว่างเซต
- A-A = ∅
- A-∅ = A
- ∅-A = ∅
- A-A’ = A
- A-U =∅
- A-B ⊂ A
- A-B = A ก็ต่อเมื่อ A∩B = ∅
- A-B = ∅ ก็ต่อเมื่อ A⊂B

จำนวนของสมาชิกของเซตจำกัด
2 เซต
n(A∪B) = n(A)+n(B)-n(A∩B)
3 เซต
n(A∪B∪C) = n(A)+n(B)+n(C)-n(A∩B)-n(A∩C)-n(B∩C)+n(A-n(A∩B∩C)


