พหุนาม ( Polynomial )

เนื้อหา พหุนาม เป็นเนื้อหาโดยสรุปในเรื่องของการหา พจน์ของพหุนาม พหุนามในรูปผลสำเร็จ ดีกรีของพหุนาม ซึ่งจะอาศัยความรู้เรื่องเอกนามเข้ามาประยุกต์ ทำให้เกิดความเข้าใจมากยิ่งขึ้น ถ้าเกิดใครยังไม่ได้ทบทวนเรื่องเอกนาม สามารถกลับไปทบทวนเรื่องเอกนามก่อนที่จะเข้าสู่บทเรียนเรื่องนี้กันครับ
เนื้อหาทั้งหมดของ พหุนาม
ดูเนื้อหาพหุนามบน YOUTUBE
พหุนาม ( Polynomial )
คือ ผลบวกหรือลบกันของเอกนามอย่างน้อยหนึ่งตัว
ศัพท์ที่ควรรู้
ศัพท์ | ความหมาย |
พจน์ของพหุนาม | เอกนามแต่ละตัวที่อยู่ในพหุนาม |
พหุนามในรูปผลสำเร็จ | พหุนามที่ไม่สามารถลดรูปได้แล้ว |
ดีกรีของพหุนาม | ผลบวกของเลขชี้กำลังเอกนามที่มีเลขชี้กำลังสูงสุดของพหุนามที่เป็นรูปผลสำเร็จ |

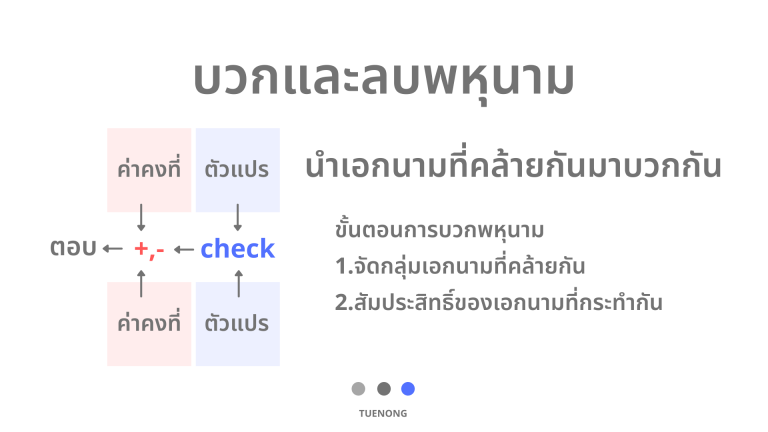
การบวก/ลบพหุนาม
การบวก/ลบพหุนาม ยังใช้กฎเหล็กข้อเดียวกับเอกนาม คือ
พหุนามจะสามารถบวกหรือลบกันได้ เมื่อตัวแปรเหมือนกัน
การบวกลบพหุนามยังช่วยให้สามารถหาพหุนามในรูปผลสำเร็จได้
ตัวอย่าง | |
4xy+5x2y-2xy | |
พหุนามในรูปผลสำเร็จ | ดีกรีของพหุนาม |
= (4-2)xy + 5x2y = 2xy + 5x2y | 2+1 = 3 (เอกนามที่มีผลบวกเลขชี้กำลังสูงสุด คือ 5x2y) |
ตัวอย่าง | |
xy2+3x2y-5xy2-x2y | |
พหุนามในรูปผลสำเร็จ | ดีกรีของพหุนาม |
= (1-5)xy2 + (3-1)x2y = -4xy2 + 2x2y | 2+1 = 3 (เอกนามที่มีผลบวกของเลขชี้กำลังสูงสุด คือ -4xy2 และ 2x2y ซึ่งมีค่าเท่ากัน) |
ลองทำโจทย์ตัวอย่าง การบวก การลบ พหุนาม ก่อนไหม คลิ้กเลย

การคูณพหุนาม
การคูณเอกนามด้วยเอกนาม
เป็นพื้นฐานในการคูณต่อ ๆ ไปหลังจากนั้น โดยหลักการคูณ เอกนามด้วยเอกนาม คือ
ตัวแปรคูณตัวแปร ค่าคงตัวคูณค่าคงตัว
กล่าวคือ ถ้าเจอเอกนาม ให้นำตัวแปรคูณกับตัวแปร ค่าคงตัวคูณกับค่าคงตัว หรือพูดสั้น ๆ ว่าประเภทเดียวกันคูณกัน ถ้ายังแยกตัวแปรกับค่าคงตัวไม่ออกสามารถไปทวนได้ที่หัวข้อแรก และ การคูณตัวแปรจำเป็นต้องใช้ความรู้เรื่องเลขยกกำลัง เพราะฉะนั้นสามารถกลับไปทวนเรื่องเลขยกกำลังได้
ตัวอย่าง
(5y2)(4y)
= (5∙4)(y2∙y)
= 20y3
ตัวอย่าง
(3a2b)(-7b3c)
= (3)(-7) (a2∙b∙b3∙c )
= -21a2b4c

การคูณเอกนามด้วยพหุนาม
: การคูณแบบนี้ต้องใช้ความรู้เกี่ยวกับสมบัติการแจงแจก โดยการกระจายเอกนามเข้าไปคูณในแต่ละพจน์ของพหุนาม
ตัวอย่าง
(5y2)(4y-3x)
= (5y2)(4y) + (5y2)(-3x)
=(4∙5)(y2∙y) + (5)∙(-3)(y2∙x)
= 20y3-15xy2
การคูณพหุนามด้วยพหุนาม
: การคูณลักษณะนี้ใช้ความรู้เกี่ยวกับสมบัติการแจกแจงเช่นกัน แต่ต่างกัน คือ ต้องให้แต่ละพจน์ของพหุนามคูณกันให้ครบทุกตัว
ตัวอย่าง
(5y2+3)(4y-3x)
= (5y2)(4y) + (5y2)(-3x) + (3)(4y) + (3)(-3x)
=(5∙4)(y2∙y)+ (5)(-3)(y2∙x)+(3∙4)y+(3)(-3)x
= 20y3-15xy2+12y-9x

การหารพหุนาม
การหารเอกนามด้วยเอกนาม
: การหารเอกนามใช้หลักการเดียวกับการคูณเลย คือ
ตัวแปรหารตัวแปร ค่าคงตัวหารค่าคงตัว
ในการหารพหุนามยิ่งมีความจำเป็นที่จะต้องทวนเรื่องเลขยกกำลัง เพื่อให้เข้าใจและสามารถทำได้อย่างถูกต้องและรวดเร็ว
(18a3) ÷ (3a)
= (18 ÷ 3 )(a3 ÷ a )
= 6 (a3-1 )
= 6a2
หมายเหตุ : ในการหารตัวแปรต้องใช้สมบัติของเลขยกำลังเข้ามาช่วยในการหาร
การหารพหุนามด้วยเอกนาม
การทำรูปแบบนี้ก็ยังมีลักษณะเดียวกันกับ การคูณเอกนามด้วยพหุนาม โดยการหารต้องใช้ความรู้เกี่ยวกับสมบัติการแจงแจก โดยการกระจายเอกนามเข้าไปหารในแต่ละพจน์ของพหุนาม
(18a3+9a) ÷ (3a)
= [(18a3)÷ (3a)] + [(9a) ÷ (3a)]
= (18 ÷ 3 )(a3 ÷ a ) + (9 ÷ 3 )(a ÷ a )
= 6 (a3-1 ) + 3 (a1-1 )
= 6a2+3
การหารพหุนามด้วยพหุนาม : การหารพหุนามด้วยพหุนามจำเป็นต้องใช้ความรู้เกี่ยวกับการหารยาว ซึ่งต้องใช้เวลาจึงจะขออธิบายเป็นอีกบทความหนึ่งในโอกาสต่อไป

