การเคลื่อนที่แบบวงกลม

การเคลื่อนที่แบบวงกลม คืออะไร ?
บทนี้จะกล่าวถึง การเคลื่อนที่แบบวงกลม นั่นคือ วัตถุที่เคลื่อนที่เป็นวงกลม บนระนาบใดๆ อัตราเร็วขณะใดขณะหนึ่งของวัตถุจะคงที่หรือไม่ก็ได้ แต่ความเร็วของวัตถุไม่คงที่แน่นอน เนื่องจากว่ามีการเปลี่ยนทิศาทางของการเคลื่อนที่ ตลอดเวลา ซึ่งเมื่อวัตถุที่มีการเปลี่ยนทิศทางการเคลื่อนที่แสดงว่า วัตถุนี้ต้องมีองค์ประกอบของแรงมากระทาในทิศทางที่ตั้งฉากกับเส้นทางการเคลื่อนที่ด้วย และกรณีที่การเคลื่อนที่มีอัตราเร็วไม่คงที่ แสดงว่าต้องมีองค์ประกอบของแรงในทิศทางที่ขนานกับแนวการเคลื่อนที่ด้วย จึงเรียกว่า การเคลื่อนที่แบบวงกลม พิจารณารูป
การเคลื่อนที่แบบวงกลม เป็นการเคลื่อนที่ของวัตถุไปตามเส้นรอบวง จะมีข้อควรทราบดังนี้
- วัตถุที่เคลื่อนที่เป็นวงกลม จะมีความเร็วเชิงมุมคงที่ แต่ความเร็วเชิงเส้นไม่คงที่ เพราะทิศทางของความเร็วเปลี่ยนแปลงตลอดเวลา
- วัตถุนั้นจะมีแรงภายนอกกระทำในทิศทางสู่ศูนย์กลางของวงกลมและตั้งฉากกับทิศทางการเคลื่อนที่เสมอ เรียกว่า แรงเข้าสู่ศูนย์กลาง (Fc)
คาบ (T)
คือ เวลาที่ใช้ในการเคลื่อนที่ครบ 1 รอบ หรือ วินาทีต่อรอบ (s)
ความถี่ (f)
คือ จำนวนรอบที่เคลื่อนที่ได้ในหนึ่งหน่วยเวลา หรือ รอบต่อวินาที (Hz)
โดยสามารถเขียนเป็นสูตรได้ว่า
f = จำนวนรอบ / เวลา
T = 1 / f
เปรียบเทียบปริมาณทางฟิสิกส์ระหว่างปริมาณเชิงเส้นและ และ เชิงมุม
ปริมาณ | เชิงเส้น | เชิงมุม |
การกระจัด | s | θ |
ความเร็ว | v | ω |
การเปลี่ยนระหว่างปริมาณเชิงเส้นเป็นเชิงมุม
โดยใช้สูตร
เชิงเส้น = เชิงมุม x รัศมี
s = θr
v = ωr
โดยที่
S คือ การกระจัดเชิงเส้น เมตร (m)
θ คือ การกระจัดเชิงมุม เรเดียน ( rad )
v คือ ความเร็วเชิงเส้น เมตรต่อวินาที( m/s )
ω คือ ความเร็วเชิงมุม เรเดียนต่อวินาที ( rad/s)
R คือ รัศมี เมตร (m)
อัตราเร็วเชิงเส้น (v)
คือ ระยะทางตามแนวเส้นรอบวงของวงกลมที่วัตถุเคลื่อนที่ได้ในหนึ่งหน่วยเวลา (m/s)
v = ωr = 2πR/T=2πRf
โดย
v คือ ความเร็วเชิงเส้น เมตรต่อวินาที( m/s )
t คือ เวลา วินาที ( s )
ω คือ ความเร็วเชิงมุม เรเดียนต่อวินาที ( rad/s)
R คือ รัศมี เมตร (m)

อัตราเร็วเชิงมุม (w)
คือ มุมที่จุดศูนย์กลางของวงกลมที่รัศมีกวาดไปได้ในหนึ่งหน่วยเวลา(เรเดียน/วินาที) rad/s
ω = θ/t = 2π/T = 2πf = v/R
โดย
θ คือ การกระจัดเชิงมุม เรเดียน ( rad )
t คือ เวลา วินาที ( s )
ω คือ ความเร็วเชิงมุม เรเดียนต่อวินาที ( rad/s)
v คือ ความเร็วเชิงเส้น เมตรต่อวินาที( m/s )
R คือ รัศมี เมตร (m)

ความเร่งเข้าสู่ศูนย์กลาง ( ac )
เป็นความเร่งเมื่อวัตถุอยู่ ณ ตำแหน่งใดก็ตามในการเคลื่อนที่แบบวงกลมจะมีความเร่งทิศเข้าสู่ศูนย์กลางเสมอ
ac = v2/r
โดย
ac = ความเร่งสู่ศูนย์กลาง เมตรต่อวินาที2 ( m/s2 )
v คือ ความเร็วเชิงเส้น เมตรต่อวินาที( m/s )
R คือ รัศมี เมตร (m)

แรงเข้าสู่ศูนย์กลาง (Centripetal Force) Fc
คือ แรงที่กระทำต่อวัตถุในการเคลื่อนที่แบบวงกลมมิทิศเดียวกับทิศของความเร่งเข้าสู่ศูนย์กลาง
Fc = mac = mv2/r = m ω2r
โดย
Fc = แรงสู่ศูนย์กลาง นิวตัน m
ac = ความเร่งสู่ศูนย์กลาง เมตรต่อวินาที2 ( m/s2 )
v คือ ความเร็วเชิงเส้น เมตรต่อวินาที( m/s )
ω คือ ความเร็วเชิงมุม เรเดียนต่อวินาที ( rad/s)
R คือ รัศมี เมตร (m)
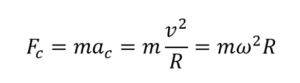
หลักการคำนวณเรื่องการเคลื่อนที่แบบวงกลมแบบต่าง ๆ
- เขียนระนาบกลมขณะที่วัตถุกำลังหมุน
- เขียนแรงที่กระทำต่อวัตถุ แล้วแตกแรงทั้งหมดให้อยู่ในแนวสู่ศูนย์กลางวงกลมและแนวตั้งฉากกับแนวสู่ศูนย์กลาง
- ในแนวสู่ศูนย์กลางหาแรงลัพธ์ที่ทีทิศทางพุ่งเข้าสู่ศูนย์กลาง แรงนี้จะทำหน้าที่เป็นแรงสู่ศูนย์กลางในแนวตั้งฉากกับระนาบวงกลมนี้ ถือว่าสมดุล ∑F ในแนวนี้เท่ากับศูนย์





